Entropixplained

This is a small guide outlining key concepts, topics, architecture, code, etc that came about as the result of my discussions with LLMs trying to understand @_xjdr's titular context aware sampler named

https://github.com/xjdr-alt/entropix

(Also known as Shrek Sampler)

Lumentis helped me turn the conversations into what you see below. Diagen helped with the diagrams. If you spot an error, drop me a note!

Jump Around

Basic Concepts

Understanding Entropy in Language Models

Attention in Transformers

Traditional Sampling Methods

Entropix System Architecture

Sampling Strategies

Dynamic Parameter Adjustment

Implementation Details

Example Generations

Intro

Entropix introduces several key innovations that set it apart from conventional sampling techniques:

Entropy-based decision making: By leveraging both entropy and varentropy of logits, Entropix can gauge the model's uncertainty and adjust sampling strategies accordingly.
Attention-aware sampling: The system incorporates metrics derived from attention patterns, such as attention entropy and agreement, to inform sampling decisions.
Dynamic parameter adjustment: Sampling parameters like temperature, top-k, and top-p are dynamically adjusted based on the current context and model state.
Adaptive multi-sample approach: In scenarios of moderate uncertainty, Entropix generates and evaluates multiple samples to select the most appropriate token.

Impact on LLM Inference

The potential impact of Entropix on language model inference is significant:

Improved coherence: By adapting to the model's uncertainty, Entropix can help maintain coherence over longer generations.
Enhanced context sensitivity: The attention-aware sampling allows for better preservation of context throughout the generation process.
Reduced hallucinations: Dynamic parameter adjustment can help mitigate hallucinations in high-uncertainty scenarios.
Flexible generation: Entropix can seamlessly transition between different sampling strategies based on the current context, allowing for more nuanced and appropriate text generation.

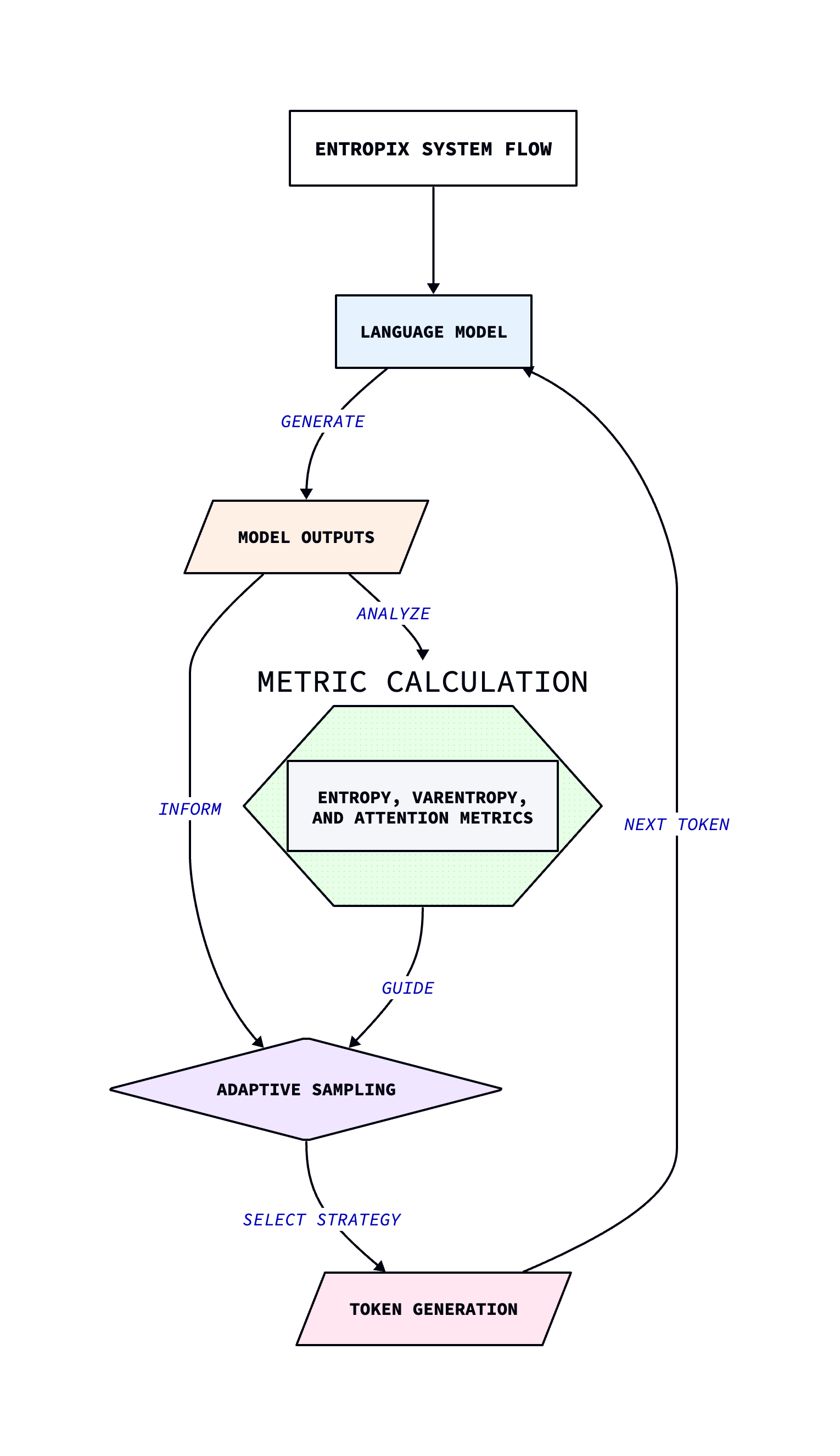
High-level flow diagram of the Entropix system showing continuous adaptation based on model output and internal state. Arrows indicate feedback loops between components including entropy calculation, attention analysis, and dynamic parameter adjustment

This diagram illustrates the high-level flow of the Entropix system, showcasing how it continuously adapts based on the model's output and internal state.

Basic Concepts

Transformer Architecture

The transformer architecture is the backbone of modern LLMs. It consists of several key components:

Embedding Layer: Converts input tokens into vector representations.
Self-Attention Layers: Allow the model to weigh the importance of different parts of the input.
Feed-Forward Layers: Process the attention outputs.
Layer Normalization: Stabilizes the learning process.

Here's a simplified diagram of a transformer block:

Token Prediction Process

When generating text, LLMs predict one token at a time. This process involves:

Step 1: Input Processing

The input text is tokenized and converted to embeddings.

Step 2: Forward Pass

The embeddings are passed through the transformer layers, producing logits for each possible next token.

Step 3: Sampling

A sampling method (which is where Entropix comes in) is used to select the next token based on the logits.

Step 4: Repeat

Steps 1-3 are repeated with the newly generated token appended to the input.

Role of Logits

Logits are the raw, unnormalized outputs of the model for each token in the vocabulary. They represent the model's "confidence" in each token being the next one in the sequence.

The logits are typically converted to probabilities using the softmax function:

P(token_i) = \frac{e^{logit_i}}{\sum_j e^{logit_j}}

These probabilities are then used in various sampling methods to select the next token.

Attention Mechanism

The attention mechanism is a key innovation in transformer models. It allows the model to focus on different parts of the input when generating each output token.

In Entropix, we utilize attention scores to calculate metrics like attention entropy and agreement, which inform our sampling strategies. More on those later.

Understanding Entropy in Language Models

Entropy, in the context of language models, measures the uncertainty or randomness in the model's predictions. It quantifies how spread out the probability distribution is over the possible next tokens.

Entropy is calculated using the following formula:

H = -\sum_{i} p_i \log_2(p_i)

Where $p_i$ is the probability of the $i$ -th token.

A high entropy value indicates that the model is uncertain about the next token, with probabilities spread across many options. Conversely, a low entropy suggests the model is more confident, with probabilities concentrated on fewer tokens.

Introducing Varentropy

Varentropy, or variance of entropy, is a measure of how much the entropy varies across different positions or contexts. It provides insight into the model's consistency in uncertainty across different parts of the input.

The calculation of varentropy involves these steps:

Step 1: Calculate entropy

Compute the entropy for each position in the sequence.

Step 2: Calculate variance

Compute the variance of these entropy values across the sequence.

Varentropy is particularly useful in identifying areas where the model's uncertainty fluctuates, which can indicate interesting or challenging parts of the text.

Significance in Sampling Decisions

The combination of entropy and varentropy plays a crucial role in Entropix's sampling strategies. Here's how they influence the decision-making process:

Low Entropy, Low Varentropy: Indicates high confidence and consistency. Entropix may use greedy sampling in these cases.
High Entropy, Low Varentropy: Suggests consistent uncertainty. This might trigger clarification insertion or increased exploration.
Low Entropy, High Varentropy: Indicates varying levels of confidence. Entropix might employ exploration sampling to investigate different possibilities.
High Entropy, High Varentropy: Represents high uncertainty and inconsistency. This scenario often leads to high uncertainty sampling with adjusted parameters.

Figure 1: Decision matrix showing how entropy and varentropy combinations determine sampling strategies. The diagram illustrates four quadrants: low entropy/low varentropy (greedy sampling), high entropy/low varentropy (clarification insertion), low entropy/high varentropy (exploration sampling), and high entropy/high varentropy (high uncertainty sampling)

Attention in Transformers

In transformer models, attention is typically implemented as multi-head attention. This means the attention mechanism is applied multiple times in parallel, allowing the model to focus on different aspects of the input simultaneously.

Attention Heads

Each attention head in a transformer model computes a set of attention scores, determining how much focus to place on different parts of the input. The number of attention heads can vary, but in the case of the Llama 1B model used in Entropix, there are 32 heads per layer:

Python
LLAMA_1B_PARAMS = ModelParams(
  n_layers=params["n_layers"],
  n_local_heads=params["n_heads"],
  n_local_kv_heads=params["n_kv_heads"],
  head_dim=params["dim"] // params["n_heads"],
  max_seq_len=params["max_seq_len"],
  rope_theta=params["rope_theta"],
  use_scaled_rope=params["use_scaled_rope"]
)

Attention Entropy

Attention entropy is a metric used in Entropix to quantify the uncertainty or spread of attention across different tokens. It's calculated using the attention probabilities:

Python
attention_probs = jax.nn.softmax(attention_scores, axis=-1)
attn_entropy = -jnp.sum(attention_probs * jnp.log2(jnp.clip(attention_probs, 1e-10, 1.0)), axis=-1)

A high attention entropy indicates that the model's attention is spread out across many tokens, while low entropy suggests the model is focusing on a few specific tokens.

Attention Agreement

Attention agreement measures how consistent the attention patterns are across different attention heads. It's calculated by comparing each head's attention distribution to the mean attention distribution:

Python
mean_attention = jnp.mean(attention_probs, axis=1)
agreement = jnp.mean(jnp.abs(attention_probs - mean_attention[:, None, :]), axis=(1, 2))

Low agreement suggests that different heads are focusing on different aspects of the input, which could indicate a complex or ambiguous context.

Relevance to Sampling

Entropix uses these attention-based metrics to inform its sampling decisions. For example:

High attention entropy might lead to increased exploration in sampling.
Low attention agreement could result in adjustments to the temperature or top-k parameters.

Interaction Strength

Interaction strength is defined as the mean of the absolute values of attention scores across all layers, heads, and positions in the transformer model. Mathematically, it can be expressed as:

\text{Interaction Strength} = \frac{1}{L \cdot H \cdot N} \sum_{l=1}^L \sum_{h=1}^H \sum_{i=1}^N \sum_{j=1}^N |A_{l,h,i,j}|

Where:

$L$ is the number of layers
$H$ is the number of attention heads
$N$ is the sequence length
$A_{l,h,i,j}$ is the attention score from position $i$ to position $j$ in head $h$ of layer $l$

Calculation Method

The interaction strength is calculated using the following steps:

Step 1: Extract Attention Scores

Obtain the raw attention scores from all layers and heads of the transformer model.

Step 2: Apply Absolute Value

Take the absolute value of all attention scores to focus on magnitude rather than direction.

Step 3: Calculate Mean

Compute the mean of these absolute values across all dimensions (layers, heads, and positions).

In the Entropix implementation, this calculation is performed efficiently using JAX:

Python
interaction_strength = jnp.mean(jnp.abs(attention_scores), axis=(1, 2, 3))

Significance in Sampling

Interaction strength plays a vital role in the adaptive sampling process of Entropix. It influences several key aspects of the sampling strategy:

Temperature Adjustment: Higher interaction strength can lead to increased temperature, promoting more diverse outputs when tokens are strongly connected.
Top-k Parameter: The interaction strength is used to dynamically adjust the top-k parameter, allowing for more or fewer candidate tokens based on the strength of token relationships.
Exploration vs. Exploitation: In scenarios with high interaction strength, the sampling strategy may lean towards more exploratory behavior to capture complex relationships between tokens.

Visualization

To better understand interaction strength, consider the following visualization of attention patterns:

In this example, the thickness of the lines represents the strength of attention. The interaction strength would be calculated by taking the mean of these absolute values (0.7, 0.2, 0.5, 0.6, 0.1, 0.8).

Impact on Text Generation

High interaction strength can indicate:

Complex relationships between tokens
Potential for more nuanced or context-dependent generation
Need for careful consideration of a wider range of token candidates

Low interaction strength might suggest:

More straightforward or independent token relationships
Potential for more focused or deterministic generation
Opportunity for more aggressive pruning of unlikely candidates

Traditional Sampling Methods

Temperature Sampling

Temperature sampling is a fundamental technique that controls the randomness of token selection. It works by scaling the logits (unnormalized prediction scores) before applying the softmax function.

The formula for temperature sampling is:

P(x_i) = \frac{\exp(z_i/T)}{\sum_j \exp(z_j/T)}

Where:

$P(x_i)$ is the probability of selecting token $i$
$z_i$ is the logit for token $i$
$T$ is the temperature parameter

Top-k Sampling

Top-k sampling restricts token selection to the k most likely tokens, where k is a predefined parameter. This method helps prevent the selection of highly improbable or nonsensical tokens.

Step 1: Sort tokens by their probabilities in descending order.

Step 2: Select the top k tokens.

Step 3: Renormalize the probabilities of these k tokens.

Step 4: Sample from this reduced set of tokens.

Top-p (Nucleus) Sampling

Top-p sampling, also known as nucleus sampling, is an adaptive approach that selects the smallest set of tokens whose cumulative probability exceeds a threshold p.

The process works as follows:

Sort tokens by probability in descending order.
Calculate the cumulative probability.
Select tokens until the cumulative probability exceeds p.
Renormalize probabilities for the selected tokens.
Sample from this dynamic set of tokens.

Top-p sampling adapts to the confidence of the model's predictions, allowing for a more flexible token selection process compared to top-k sampling.

Entropix System Architecture

Main Components

The Entropix system consists of several key components:

Language Model: The core transformer-based language model (Llama in this case).
KV-Cache: A cache for storing key and value tensors to optimize inference.
Metric Calculator: Computes entropy, varentropy, and attention-based metrics.
Sampling Strategies: A collection of specialized sampling techniques.
Adaptive Sampler: The central decision-making component that selects and applies sampling strategies.

Let's visualize how these components interact:

Data Flow and Decision-Making Process

The Entropix system follows a specific flow during text generation:

Step 1: Token Generation

The language model processes the input tokens and generates logits and attention scores.

Step 2: Metric Calculation

The Metric Calculator computes entropy, varentropy, attention entropy, attention agreement, and interaction strength based on the model outputs.

Step 3: Strategy Selection

The Adaptive Sampler analyzes the calculated metrics and selects the most appropriate sampling strategy.

Step 4: Parameter Adjustment

Based on the selected strategy and metrics, sampling parameters (temperature, top-k, top-p, min-p) are dynamically adjusted.

Step 5: Token Sampling

The chosen sampling strategy is applied to select the next token.

Step 6: Iteration

The process repeats from Step 1, incorporating the newly generated token.

Sampling Strategies

The heart of Entropix's sampling approach is its strategy selection logic. This system continuously evaluates the model's output metrics and chooses the most appropriate sampling method for each token generation step.

Adaptive Sampling

The adaptive sampling strategy kicks in when the entropy and varentropy of the logits don't fall into extreme categories (unlike scenarios that trigger specialized sampling techniques). It's designed to balance exploration and exploitation, adapting to the current context and model state.

The Adaptive Sampling Process

Step 1: Calculate Metrics

First, we calculate various metrics from the model's logits and attention scores:

Logits entropy and varentropy
Attention entropy and varentropy
Attention agreement
Interaction strength

Step 2: Adjust Sampling Parameters

Based on these metrics, we dynamically adjust the sampling parameters:

Temperature
Top-p (nucleus sampling threshold)
Top-k
Minimum probability threshold (min_p)

Step 3: Generate Multiple Samples

We generate multiple candidate tokens using the adjusted parameters. The number of samples is configurable, with a default of 12 in the current implementation.

Step 4: Score Samples

Each sample is scored based on two factors:

Log probability from the model's logits
A confidence score derived from the calculated metrics

Step 5: Select Best Sample

The sample with the highest combined score is selected as the final output token.

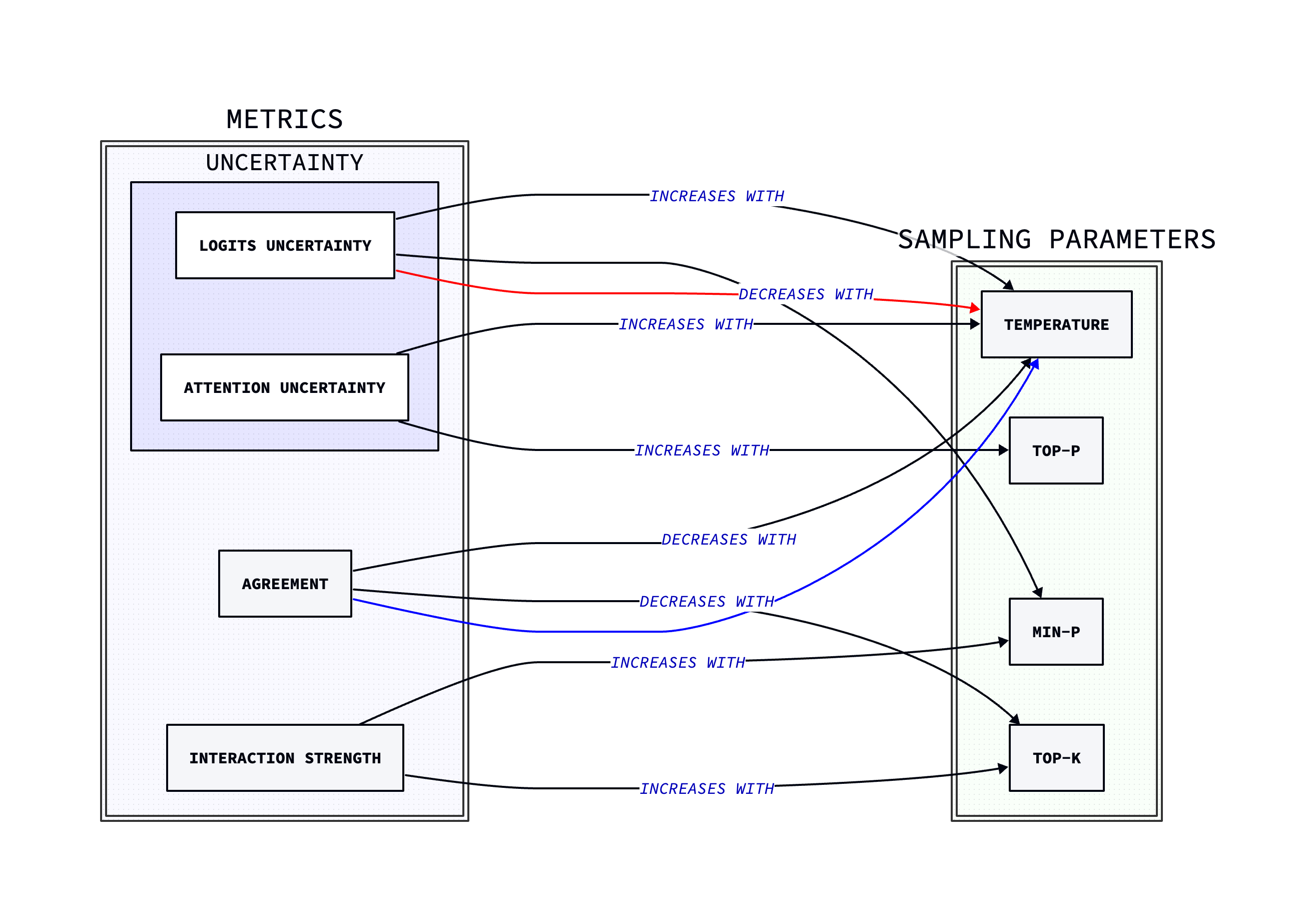
Parameter Adjustment

The heart of adaptive sampling lies in how it adjusts the sampling parameters. Let's look at each parameter:

Temperature Adjustment

Temperature is adjusted based on logits uncertainty, attention uncertainty, and agreement:

Python
temperature = base_temp * (1 + 0.3 * logits_uncertainty + 0.2 * attn_uncertainty - 0.2 * metrics["agreement"])

This formula increases temperature (more randomness) when uncertainties are high and decreases it when agreement is high.

Top-p Adjustment

The nucleus sampling threshold is modified based on attention varentropy:

Python
top_p = jnp.clip(base_top_p * (1 + 0.1 * metrics["attn_varentropy"]), 0.1, 1.0)

Top-k Adjustment

The top-k parameter is adjusted considering interaction strength and agreement:

Python
top_k = int(jnp.clip(
    jnp.round(base_top_k * (1 + 0.3 * metrics["interaction_strength"].item() - 0.2 * metrics["agreement"].item())),
    a_min=1,
    a_max=100
))

Minimum Probability Threshold

The min_p parameter is set based on logits uncertainty:

Python
min_p = jnp.clip(base_min_p * (1 - 0.5 * logits_uncertainty), 0.01, 0.5)

Sample Scoring

After generating multiple samples, each one is scored using a combination of log probability and a confidence score:

Python
def score_sample(sample):
    log_prob = jnp.sum(jax.nn.log_softmax(logits) * jax.nn.one_hot(sample, logits.shape[-1]))
    confidence_score = (
        (1 - metrics["logits_entropy"]) * 0.1 +
        (1 - metrics["attn_entropy"]) * 0.2 +
        (1 - metrics["logits_varentropy"]) * 0.3 +
        (1 - metrics["attn_varentropy"]) * 0.4 +
        metrics["agreement"] * 0.5 +
        metrics["interaction_strength"] * 0.6
    )
    return log_prob + confidence_score

This scoring function balances the likelihood of the token (log_prob) with a confidence measure derived from various metrics. The weights for each component in the confidence score can be tuned based on empirical results.

Specialized Sampling

Entropix employs a range of specialized sampling techniques to handle various scenarios encountered during text generation. These techniques are designed to adapt to different levels of entropy and varentropy, ensuring optimal token selection in diverse contexts.

Let's explore the four main specialized sampling techniques used in Entropix:

Greedy Sampling for Low Uncertainty

When both entropy and varentropy are very low, the model is highly confident about its prediction. In this case, we use greedy sampling.

Step 1: Check entropy and varentropy thresholds

Verify if both entropy and varentropy are below a certain threshold (typically 0.1).

Step 2: Select the most probable token

If the thresholds are met, simply choose the token with the highest probability.

Clarification Insertion

In scenarios with high entropy but low varentropy, the model is uncertain but consistent in its uncertainty. This might indicate a need for clarification.

Step 1: Check for high entropy, low varentropy condition

Verify if entropy is above a threshold (e.g., 3.0) and varentropy is below a threshold (e.g., 0.1).

Step 2: Insert clarification token

If the condition is met and a clarification token hasn't been recently used, insert a predefined "clarification question" token.

Step 3: Adjust sampling for follow-up

If a clarification was just inserted, use slightly higher temperature sampling for the next token.

Exploration Sampling

When entropy is low but varentropy is high, the model is confident but sees multiple distinct possibilities. This calls for exploration.

Step 1: Adjust temperature

Increase the temperature based on the interaction strength metric.

Step 2: Modify top-k

Adjust the top-k parameter based on the attention agreement metric.

Step 3: Sample with adjusted parameters

Use the modified temperature and top-k for sampling.

High Uncertainty Sampling

In cases of both high entropy and high varentropy, the model is highly uncertain and sees many possibilities. This requires a more exploratory approach.

Step 1: Significantly increase temperature

Adjust temperature based on attention varentropy.

Step 2: Modify top-p

Decrease the top-p parameter when attention entropy is high.

Step 3: Sample with adjusted parameters

Use the modified temperature and top-p for sampling.

Dynamic Parameter Adjustment

Temperature Adjustment

Temperature is a critical parameter that controls the randomness of the sampling process. In Entropix, temperature is dynamically adjusted based on several factors:

The temperature adjustment formula is:

$T = T_{base} * (1 + 0.3 * U_{logits} + 0.2 * U_{attn} - 0.2 * A)$

Where:

$T_{base}$ is the base temperature (default: 0.666)
$U_{logits}$ is the logits uncertainty (entropy + varentropy)
$U_{attn}$ is the attention uncertainty (attention entropy + attention varentropy)
$A$ is the agreement metric

This formula increases temperature when uncertainties are high (promoting exploration) and decreases it when agreement is high (promoting more focused sampling).

Top-k and Top-p Adjustment

Entropix also dynamically adjusts the top-k and top-p (nucleus sampling) parameters:

Top-k Adjustment

Python
top_k_adj = max(5, int(top_k * (1 + 0.3 * interaction_strength - 0.2 * agreement)))

This adjustment increases top-k when interaction strength is high and decreases it when agreement is high, allowing for more or fewer candidate tokens based on the model's current state.

Top-p Adjustment

Python
top_p_adj = jnp.clip(base_top_p * (1 + 0.1 * metrics["attn_varentropy"]), 0.1, 1.0)

The top-p parameter is adjusted based on attention varentropy, potentially allowing for a wider or narrower range of tokens depending on the uncertainty in attention patterns.

Minimum Probability Threshold

Entropix introduces a minimum probability threshold (min_p) that's dynamically adjusted:

Python
min_p = jnp.clip(base_min_p * (1 - 0.5 * logits_uncertainty), 0.01, 0.5)

This adjustment helps prevent the selection of extremely low probability tokens when uncertainty is high, maintaining a balance between exploration and quality.

Impact on Sampling

These dynamic adjustments work together to create a flexible sampling strategy that adapts to the current context and model state. For example:

In high uncertainty scenarios, increased temperature and top-k allow for more exploratory sampling.
When the model is more confident (low entropy, high agreement), reduced temperature and top-k lead to more focused sampling.
The adaptive min_p helps maintain coherence even in highly uncertain situations.

Implementation Details

Metrics Calculation

All these metrics are calculated in the calculate_metrics function:

Python
def calculate_metrics(logits: jnp.ndarray, attention_scores: jnp.ndarray) -> Dict[str, jnp.ndarray]:
    entropy, varentropy = calculate_varentropy_logsoftmax(logits)

    attention_probs = jax.nn.softmax(attention_scores, axis=-1)
    attn_entropy = -jnp.sum(attention_probs * jnp.log2(jnp.clip(attention_probs, 1e-10, 1.0)), axis=-1)
    attn_varentropy = jnp.var(attn_entropy, axis=-1)

    mean_attention = jnp.mean(attention_probs, axis=1)
    agreement = jnp.mean(jnp.abs(attention_probs - mean_attention[:, None, :]), axis=(1, 2))

    interaction_strength = jnp.mean(jnp.abs(attention_scores), axis=(1, 2, 3))

    return {
        "logits_entropy": jnp.mean(entropy),
        "logits_varentropy": jnp.mean(varentropy),
        "attn_entropy": jnp.mean(attn_entropy),
        "attn_varentropy": jnp.mean(attn_varentropy),
        "agreement": jnp.mean(agreement),
        "interaction_strength": interaction_strength
    }

Transformer Model Modifications

Attention Score Extraction

One of the key modifications is extracting attention scores from each layer of the transformer. This allows us to compute attention-based metrics such as attention entropy, agreement, and interaction strength.

AttnStats

Create an AttnStats class to store and update attention-related metrics across layers:

Python
class AttnStats(NamedTuple):
  entropy: jax.Array  # (bsz, n_layers, num_heads)
  varentropy: jax.Array  # (bsz, n_layers, num_heads)
  n_layers: int
  n_heads: int

  # ... methods for updating and calculating stats

Logit Processing

To calculate entropy and varentropy of logits, we need to modify the model's forward pass to expose the logits before they're converted to probabilities.

Python
def xfmr(xfmr_weights, model_params, tokens, cur_pos, freqs_cis, kvcache, attn_mask=None):
    # ... (earlier parts of the function)

    logits = jnp.dot(rms_norm(h, xfmr_weights.norm), xfmr_weights.output.T)
    return logits, kvcache, scores, attn_stats

This modification allows us to access raw logits for entropy calculations and subsequent sampling decisions.

Integration with KV-Cache

Entropix needs to work efficiently with the model's key-value cache to support fast autoregressive generation. We integrate the KV-cache management directly into the transformer implementation:

Python
def attention(x, layer_weights, model_params, cur_pos, layer_idx, freqs_cis, kvcache, attn_mask=None):
    # ... (attention calculation)

    keys, values, kvcache = kvcache.update(xk, xv, layer_idx, cur_pos, n_rep)

    # ... (rest of attention computation)

    return out, kvcache, pre_scores

This integration ensures that Entropix can leverage the efficiency gains of KV-caching while still accessing the necessary information for its sampling decisions.

Metric Calculation Pipeline

To make Entropix's sampling decisions, we need to calculate various metrics during the forward pass. We integrate this metric calculation directly into the transformer's execution:

Python
def xfmr(xfmr_weights, model_params, tokens, cur_pos, freqs_cis, kvcache, attn_mask=None):
    # ... (model execution)

    for i in range(model_params.n_layers):
        # ... (layer computation)
        attn_stats = attn_stats.update(scores[:,:,-1,:], i)

    # ... (final logits calculation)

    return logits, kvcache, scores, attn_stats

This integration allows us to accumulate attention statistics across layers, which are then used in the sampling process.

Example Generations

Low Uncertainty Generation

Let's start with a scenario where the model is highly confident in its predictions.

Step 1: Metric Calculation

The system calculates the entropy and varentropy of the logits:

Entropy: 0.05
Varentropy: 0.02

Step 2: Strategy Selection

Given the low entropy and varentropy, Entropix selects the greedy sampling strategy.

Step 3: Token Generation

The system simply selects the token with the highest probability.

In this scenario, the model might be completing a common phrase or generating text in a familiar context. For example:

Text

Input: "The capital of France is"
Output: " Paris"

The model is extremely confident about this fact, resulting in low entropy and varentropy.

High Entropy, Low Varentropy Scenario

This scenario represents a case where the model is uncertain but consistently so across all tokens.

Step 1: Metric Calculation

Entropy: 3.5
Varentropy: 0.08

Step 2: Strategy Selection

The high entropy and low varentropy trigger the clarification insertion strategy.

Step 3: Token Generation

Entropix inserts a clarifying question token (if not already present) or samples with slightly higher temperature.

This scenario might occur when the model needs more context to proceed confidently. For example:

Text

Input: "The best programming language for"
Output: " [CLARIFY] What specific task or criteria are you considering?"

Here, the model recognizes that the question is too broad and requires clarification before providing a meaningful answer.

Exploration Scenario

In this case, the model is relatively confident overall but sees multiple distinct possibilities.

Step 1: Metric Calculation

Entropy: 2.1
Varentropy: 5.5
Interaction Strength: 0.8

Step 2: Strategy Selection

The low entropy and high varentropy trigger the exploration sampling strategy.

Step 3: Parameter Adjustment

Entropix adjusts the temperature and top-k parameters:

Temperature adjustment: $1.2 + 0.3 * 0.8 = 1.44$
Top-k adjustment: Increases based on the agreement metric

Step 4: Token Generation

The system samples using the adjusted parameters, encouraging exploration of different possibilities.

This scenario might occur when the model is generating creative content or considering multiple valid continuations. For example:

Text

Input: "The detective entered the room and saw"
Output: " a mysterious"

The model might be considering various intriguing objects or scenes, leading to high varentropy despite relatively low overall entropy.

High Uncertainty Scenario

This scenario represents a case where the model is highly uncertain across the board.

Step 1: Metric Calculation

Entropy: 5.5
Varentropy: 5.2
Attention Varentropy: 0.9

Step 2: Strategy Selection

The high entropy and high varentropy trigger the high uncertainty sampling strategy.

Step 3: Parameter Adjustment

Entropix significantly adjusts the sampling parameters:

Temperature adjustment: $2.0 + 0.5 * 0.9 = 2.45$
Top-p adjustment: Decreases based on attention entropy

Step 4: Token Generation

The system samples using the highly adjusted parameters, allowing for more randomness and diversity in the output.

This scenario might occur when the model is dealing with unfamiliar or ambiguous contexts. For example:

Text

Input: "The quantum fluctuations in the hyperdimensional manifold caused"
Output: " an unexpected"

Here, the model is dealing with a complex and potentially nonsensical input, leading to high uncertainty across all metrics.

Adaptive Sampling Scenario

In cases that don't fall into the extreme categories, Entropix uses its adaptive multi-sample approach.

Step 1: Metric Calculation

Logits Entropy: 2.8
Logits Varentropy: 1.5
Attention Entropy: 1.9
Attention Varentropy: 0.7
Agreement: 0.6
Interaction Strength: 0.75

Step 2: Parameter Adjustment

Entropix adjusts all sampling parameters based on the calculated metrics:

Temperature
Top-p
Top-k
Minimum probability threshold

Step 3: Multi-sample Generation

The system generates multiple samples (default is 12) using the adjusted parameters.

Step 4: Sample Scoring

Each sample is scored based on its log probability and a confidence score derived from the metrics.

Step 5: Token Selection

The highest-scoring sample is selected as the final output.